Sub-Light Travel: Getting Around in Traveller
This article originally appeared in the May/June 2022 issue.
Many of us at one time or another have dreamed of traveling to another world. Unfortunately the best most of us have been able to do is to travel in our imagination. In Traveller, of course, sophonts often reach another planet using jump engines. Most of the time there really isn’t a practical alternative. However there are many resources within a single planetary system that are accessible to gravitic drives. Asteroid miners, hydrocarbon extractors, sophonts with more than one semi-habitable planet in their system, and gas skimming freighter pilots all have very good reasons for not using jump engines. In the TV show The Expanse, for example, humans have interests on Earth, Mars, asteroids, Jovian moons, and a blue-goo Gate somewhere out beyond Uranus. Finally, the idea of sleeper ships, sub-light ships that can reach star systems light years away, are also a common feature of early space travel. This article addresses a few of the issues when sub-light travel is the best (or only) way to travel.
The Basic Physics
In-system travel in Traveller relies on good old Newtonian physics, where the distance traveled under constant acceleration is given by the formula d=½at2. However, ships can only accelerate half of the way to their destination and spend the other half decelerating since arriving at a planet at terminal velocity generally ends badly for both ship and planet. Using this fact and rearranging Newton’s formula gives t=2√(d/a).
Note that this formula assumes constant acceleration, and this is exactly what gravitic propulsion provides: a reactionless (i.e., no mass expelled from the vessel) drive. This is very different from current (OK, real) interplanetary drives that have to push mass out one end of the ship to accelerate the ship in the other direction. Reaction drive vessels therefore spend the vast majority of their travel time in unpowered flight because they simply cannot carry enough mass with them to provide constant acceleration. For this reason, most Traveller players ignore real world methods like Hohmann transfers, gravitational slingshots, or atmospheric braking in their games. This greatly simplifies the calculations and works because gravitic drives do not need to follow all of Newton’s Laws.
Why Travel Sub-Light Anyway?
Given the versatility of Jump capable ships, it’s not surprising interstellar trade and even some in-system trade use these vessels. Sub-light ships do have several advantages. First, maneuver drives are much more efficient in their use of hydrogen. Every jump, even in system jumps, require 10 tons of hydrogen per 100 tons of ship and takes about 1 week. Maneuver drives require a fraction of that, and in addition take less time for journeys to even moderately distant worlds. For low value cargo that is not time sensitive, sub-light ships on a boring journey between distant worlds may still be more economical than jumping from place to place.
Secondly, jump engines are expensive to procure, service, and take up valuable space aboard ship. An inexpensive cargo vessel that carries a higher percentage of cargo per ton of ship can make more money per trip than a more expensive jump capable vessel. Cutting out the extra expense and space of jump engines and their extensive fuel requirement allows a greater percentage of the ship to be used for its intended purpose, whether it be cargo, research, or military defense.
Technology level may be another reason sub-light vessels are the primary space vehicle for a particular system. Gravitic drives generally appear one tech level before jump technology. A planet that develops efficient space flight is unlikely to remain bound to their planet of origin when other worlds become accessible. Even if they are not habitable, mining operations and scientific exploration would likely drive many dreamers to visit other planets. Modern day Earth currently has plenty of such visionaries.
Some systems may make extensive use of sub-light ships for self sufficiency. Starships require a Class A starport to build, and a shipyard of that caliber is expensive to maintain. Sub-light craft, particularly the omnipresent modular cutter, can be built in a class B or C starport. A system that produces more of its own requirements is more independent. For some governments independence alone would be enough to justify sub-light ships. Monitors, sub-light warships used extensively for system defense, may be the only way some systems maintain their autonomy in the face of an aggressive neighbor with Jump technology.
Finally, many polities have uncounted numbers of small operations scattered in valuable sites around the solar system. Whether they’re mining operations in an asteroid belt, fuel skimming operations around gas giants, or research stations on lifeless worlds, bases require supplies. Sub-light ships can deliver smallish quantities of personnel and supplies more efficiently than any jump capable transport can. For minor operations struggling to make a profit, reduced logistics costs could mean the difference between success and failure.
The Distance Problem
So going back to the usual Traveller formula, there are 3 variables in sub-light travel: acceleration, distance, and time. Acceleration is given by the gravitic drives and measured in gravities, where 1g is approximated as 10 m/sec2. Distance is how far two objects (or points in space) are from one another, with time being the unit travelers want to know. Easy, right? OK, maybe not; we may know where we want to travel, but that destination body (and our starting location) are moving independently and the distance between those bodies is not constant. Planets within the habitable zone of a red dwarf star, for example, must be fairly close to the star and therefore have a relatively short period. A short period means that the planet must cover its entire orbit over that time, often less than a month. If the planet has a period of 30 days, it will thus have to travel 12 degrees around its orbit in only one day. The shorter the planetary ‘year’, the higher percentage of the circle a planet travels per day. A spacecraft trying to reach that planet will have to navigate to where the planet will be when it arrives rather than where the planet was when the journey started. Note that a lot of referees (including myself) ignore this detail when planning sub-light trips.
Kepler’s first law of planetary motion partially says that planetary bodies have elliptical orbits around their primaries. These orbits can often be approximated as a circle with a radius of the semi-major axis (average of the shorter and longer axes of the ellipse). Eccentricity is a measure of how far from circular an orbit is, and most planetary bodies in our solar system vary by less than 10%. As examples, the eccentricity of Luna’s orbit around Earth is 0.055, the Earth’s orbit around the Sun is 0.017, Mars is 0.093, and Jupiter’s is 0.048. Exoplanets and small bodies (planetoids, comets, minor planets, etc) seem to have more variable eccentricities, so this may not apply to all solar systems. Circles just make calculations easier. Figure 1 shows what the different eccentricities look like compared to one another.
The other half of Kepler’s first law states that each planetary body sweeps out equal areas in equal time. In practice, this means that outer planets move more slowly the further they are from the sun. Planning a trip to that planet, then, would require knowing exactly where a planet is in its orbit so that its relative motion can be taken into account. Kepler’s third law gives a mathematical description of this, where the cube of the semi-major axis (approximate radius of the orbit) is proportional to the square of the period of rotation. With circular orbits the planet’s speed is constant and life is simpler. A great demonstration of how this works with orbits of different eccentricities but the same average distance can be found in Wikipedia’s entry on orbital eccentricity.
Note that the planetary orbits around the Sun are usually described as circles despite the fact that space is three dimensional. Our solar system’s planets mostly lie in a plane known as the ecliptic, which passes through the sun and close to all of the major planets. This is also true of many major moons in our solar system which often have their own ecliptic plane based around the rotation of the planet. This orientation is believed to have been generated during the formation of the solar system as dust and gasses spun around the proto- planetary disk which eventually condensed into the sun and planets. Moons which are not found in the ecliptic are thought to have been captured after the formation of the planets. For Traveller purposes, the ecliptic makes life better as two-dimensional calculations are easier than three dimensions.
There are still more assumptions we can make to simplify the mathematics and create a semi-realistic situation while maintaining playability. For example, in an era of interstellar travel and extensive space commerce, going from Earth to Mars should be relatively simple. How long such a trip will take depends upon the acceleration of the ship and the actual distance between the planets. Analyzing a few basic orbital positions can give us a good feel for what the key issues are.
Earth orbits the sun at an average distance of roughly 150 million km, or 1.5×1011 meters with an eccentricity of 0.017. For Mars, the key values are 2.28×1011 meters and an eccentricity of 0.093. On average, therefore, Mars and Earth are 7.8×1010 meters apart when they are nearest one another. Because of the orbital eccentricities, that can vary from an absolute minimum of 5.4×1010 meters and a relative minimum of 1.03×1011 meters, which is nearly twice as distant. In terms of time it takes to travel at 1g acceleration, applying t=2√(d/a) gives 146,986 seconds, or 40.82 hours at absolute closest approach, 176,634 seconds or 49.07 hours at an average distance, and 101,488 seconds or 56.38 hours when the Earth/Mars pair are relatively close but at opposite ends of their eccentricities. Therefore the trip would vary by nearly 16 hours at the extremes, but most of the time would take about two days at 1g constant acceleration. For higher accelerations, simply divide the time by the square root of the M-drive rating; thus a 4g acceleration would cut the time to just slightly more than a day between Earth and Mars. This is much preferable to a week-long jump.
When Earth and Mars are on opposite sides of the sun they average 3.78×1011 meters apart, with a maximum of 4.02×1011 meters and a minimum of 3.49×1011 meters. At 1g constant acceleration, it would take between 103.78 and 111.39 hours, with an average of 108.01 hours, roughly 4.50 days, to go from Earth to Mars when they are at their most distant. This means that for the case of Earth and Mars, the minimum and maximum travel time can vary by over 100% depending upon where in their orbits the two planets happen to be.
This set of calculations illustrates two additional points. First, the relative orbital positions are substantially more important than orbital eccentricity. When Earth and Mars are at their most distant, it takes an average of 108.01 hours (4.50 days), while eccentricity only changes the time by about 8 hours either way at 1g, with even shorter time differences for ships with higher accelerations. Secondly, as overall distance increases the same percentage change in distance causes less variation in the time it takes to cover the distance. Since acceleration is constant, more of the time is spent going at higher velocities. While the travel time difference is just under 16 hours at the shortest and longest closest approach, the times are slightly less than 8 hours apart when the planets are at their most distant.
During an actual game, unless a referee is willing to calculate the orbital eccentricity and exact orbital positions for each planet for every trip players take between planets, some compromises between accuracy and simplicity must be made. One simple assumption is that orbits are circular as opposed to elliptical. This is actually pretty close to true, as many planets have eccentricities that are less than 5%. Mars is actually on the high end in the eccentricity scale and is relatively close to Earth, both of which contribute to this being an extreme example for differences between absolute minimum and relatively distant minimums. Exoplanets are known to have greater orbital eccentricities, but how common or how stable these examples are remain to be seen. (The fact that they could even find 5000+ exoplanets currently still blows my mind, let alone calculate orbits!)
This circularity is important for estimating the average distance between any two planets. For a circular orbit, the angular velocity of the planet is the same at all points in its orbit and the average position of the planet is simply the center of the circle which is the sun. In a true orbit, the sun is at one focus of the ellipse, the planet has a higher angular velocity when it is closer to the sun, and it spends less time close to the sun. Therefore not only is a planet further from the sun, it moves more slowly when it is further away in its orbit, increasing the time the planet spends at its more distant points. With a circle, these problems are completely avoided and leave calculations much simpler.
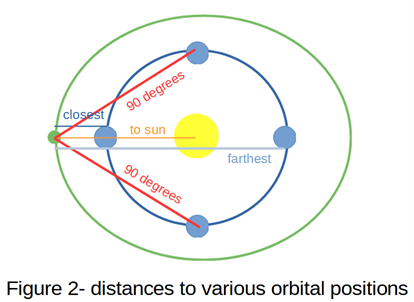
For circular orbits, the average distance between two planets is simply the outermost planet’s distance from the sun. We can test this assumption using several simple cases diagrammed in Figure 2. Mars is 49.07 hours distant at closest average approach, and 108.01 hours apart at its most distant as described above. When Mars and Earth are oriented at 90 degrees to one another, the Earth-Mars-Sun form a right triangle, with the two shorter sides being the Mars-Sun and Earth-Sun distances. From good old Pythagoras, we know that a2+b2=c2 (where c is the hypotenuse, and thus the distance between Earth and Mars) and so the distance between Earth and Mars is roughly 272.9 million kilometers. This gives a travel time of 90.65 hours at 1g when the planets are at right angles to one another. Taking the average travel time to these four positions (closest, farthest, and 2×90 degrees) gives an average transit time of 84.60 hours. The average time it would take to travel from Mars to the Sun would be 82.40 hours, a rather close approximation.
The same assumption works for any set of planets that have an approximately circular orbit, where the average time from one planet to another is roughly the same as from the most distant planet to the Sun. The table below gives the time in hours it takes to get from the listed planet to Earth or the Sun at the same positions as detailed in the Mars example above using 1g acceleration. In all cases, the average time to Earth is very nearly the same time it would take to travel from the planet in question to the Sun. Thus the average interplanetary travel time between any two orbits is approximately the time it takes to travel from the most distant planetary body to its star. This greatly simplifies the referee’s calculations while keeping the concept that it takes more time to get to more distant worlds within the solar system.
| Travel Times (in Hours) Between Solar System Planets and Earth (note 1) | |||||
|---|---|---|---|---|---|
|
Times to Earth when distance is... |
|||||
| Originating planet | Minimum | Hypoteneuse (note 3) |
Maximum | Average | Time from planet to Sun (note 4) |
| Mercury | 52.70 | 70.61 | 80.51 | 68.61 | 68.04 |
| Venus | 39.28 | 74.59 | 87.84 | 69.08 | 68.04 |
| Mars | 46.48 | 90.65 | 106.86 | 83.66 | 82.40 |
| Asteroids (note 2) | 90.44 | 116.70 | 132.05 | 113.97 | 113.18 |
| Jupiter | 139.44 | 156.57 | 169.42 | 155.50 | 155.16 |
| Saturn | 197.98 | 209.93 | 220.13 | 209.49 | 209.35 |
| Uranus | 289.74 | 297.83 | 305.30 | 297.68 | 297.62 |
| Neptune | 183.21 | 186.39 | 189.42 | 186.35 | 186.34 |
| note 1 Uses distances given in
https://en.wikipedia.org/wiki/Solar_System, which differ
somewhat from the Earth and Mars figures used earlier. note 2 This uses the average distance to the middle of the belt, 4.15×108 km note 3 Defined as the distance between the planets when they are 90° apart as seen from the sun note 4 If the planet is closer to the sun than Earth, this is the time from Earth to the sun |
|||||
Planetoids Sharing the Same Orbit
This analysis breaks down, however, when dealing with bases in an asteroid belt. As all of the bodies are at (roughly) the same orbital distance from the Sun, some bodies are going to be much closer to one another than others. It is likely true that the average times to different bases in an asteroid belt are about the same as the time it takes to reach the Sun (assuming an equal distribution of bases throughout the belt), but some bases by chance will be closer together than others. A game set in an asteroid belt or where various bases in an asteroid belt play a major role could justify calculating different travel times between various asteroid bases. If the asteroids bases play only a minor role, then assuming travel time to the sun between bases is probably adequate.
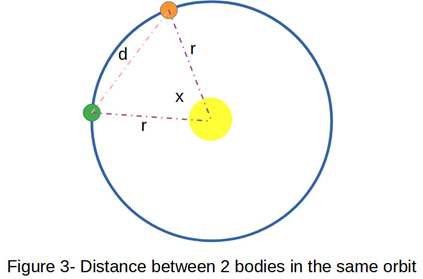
For a more nuanced description, however, geometry again provides a reasonable distance approximation assuming a circular orbit for all of the asteroids at a single distance from the star. (No, this will not happen in any real life system; for the purposes of approximation, though, this likely gets pretty close to the actual travel time.) Given two planetoids with the same circular orbit separated by x degrees, one can draw a triangle between the two planetoids and the sun where the distance d between the two planetoids is opposite the angle x. Next, draw an imaginary line that bisects angle x; because the two planetoids are in the same circular orbit those sides of the triangle are equal and the bisecting line forms a right angle to the line connecting the two planetoids as shown in Figure 3.
This creates two right triangles, where the hypotenuse is the planetoid belt’s orbital distance from the sun (r), the angle with the vertex at the Sun is ½x and the opposite side of the right triangle is ½d, the distance between the two planetoids. From geometry again, ½d = r×sin ½x, or d= 2r×sin ½x after rearrangement. This gives a fairly accurate distance between any two bodies occupying approximately the same circular orbit as long as the orbital radius and their degree of separation are known.
These calculations may also be useful for other situations where objects share the same circular orbit. For example, based on the three-body problem of physics, there are five spatial positions known as Lagrange points where the gravitational forces of two large bodies cooperatively balance the centripetal force of the orbital motion about a star. Two of the Lagrange points are located 60 degrees in advance of and trailing planetary bodies where planets or planetoids may share a stable orbit. Jupiter has large collections of asteroids around both of its Lagrange points known as Trojan asteroids, although Saturn and other planets (including Earth!) have their own Trojans. Given the radius of Jupiter’s orbit (778 million km) and 60 degrees orbital separation, the distance between Jupiter and it's Lagrange asteroids is 2 × 7.78×108×sin (0.5×60) = 7.78×108 km which is exactly the distance of Jupiter to the Sun. The Trojan asteroids (of any planet, not just Jupiter) follow odd semi-elliptical orbits around their Lagrange point, but this approximate distance is easily a close enough for most Traveller referees.
Distant Binary Stars
Approximately one-third of all stellar systems in the Milky Way are believed to contain multiple stars. Most multiple star systems are binaries, with fewer systems possessing three, four, or even more separate stellar entities. Based on current exoplanet studies, at least 100 binary star systems have at least one planet in them, suggesting that planets in binary star systems are reasonably common. P-type orbits where the planet orbits both stars are the least common orbit and require the two stars to be a close binary pair. Planets with the more common S-type orbit circle one of the stars and (mostly) ignore the stellar companion. A useful summary of how planetary systems around binary stars might be stable is found in Astronomy and Astrophysics, 434(1): 355-64, 2005.
For many binary systems, then, gravitic drives may be perfectly adequate to reach a second set of planets that orbit around another very nearby star. The next question is how long does it take to reach the other star system? Most referees do not have the time or patience to determine the exact orbital positions of all the planets in the two star systems. Fortunately, the same approximations that work between planets work between solar systems (or moons orbiting different planets) as well. By assuming the average distance between two planets orbiting nearby stars is essentially the same as the distance between the two stars themselves, it becomes very easy to calculate how long it would take to travel to another planet in the neighboring system.
Binary stars vary in how far apart they are. If close binaries have planets, they will be in P-type elliptical orbits around the common center of mass for the two stars. More distant binaries are in the tens to thousands of astronomical units (AU), with very distant binaries over a light year apart. For reasonably distant binaries, a 20 AU (3,000 million km) trip would take 304.3 hours (12.68 days) while 200 AU distant partners would take 962.3 hours or 5.7 weeks at 1g for a one-way journey. For 2000 AU, travel time would be an unpleasantly long 18.1 weeks between them. Higher acceleration maneuver drives will shorten the transit time but increase the fuel consumption.
Jump travel clearly makes sense between very distant binary systems even when time is not an important consideration. Low priority, low value cargo, however, may take the slow route when cost vs. time tradeoffs are advantageous. A familiar example can be found when crossing oceans on Earth. Priority expensive cargoes such as computer chips can get from Asia to the United States in hours by air, but cheap shoes or clothes produced in Asian sweatshops come by ocean freighter in weeks. It isn’t economically sensible to use fast transport for inexpensive products. For systems with lower technology levels or only a Class B starport, sub-light travel may be the preferred (or only) way of getting to their stellar neighbors.
Interstellar Sub-Light Travel
Sub-light generation ships are a staple of science fiction. The generation ships provide an environment where the crews can live for decades or even centuries as the ship slowly travels the vast distances between the stars. Some stories have entire communities live and die within giant spacecraft, in some cases never even realizing there is anything beyond their enclosed world. “For the World is Hollow, and I have Touched the Sky” was an original Star Trek episode which used this plot, but there are many examples. In any event, the idea of reaching another world, another star system, even in some future time when the original passengers are long dead, excites many who might otherwise write off space travel as an expensive indulgence.
This is where gravitic engines can really strut their stuff. They may be completely outclassed by Jump capable vessels, but for a low-ish tech system with spaceflight and gravitic engines but nothing beyond them, the stars still beckon explorers onward. Newtonian physics tells us that v (velocity) equals acceleration (a) times time (t). The closer one gets to the speed of light the faster a destination can be reached, but relativity changes the equation massively and is best avoided. For many writers, a significant fraction (50%?) of the speed of light is a common upper limit for physical sub-light travel, but your universe might be different.
So how long does it take a 1g maneuver drive to reach 50% of the speed of light? 10 meters per second per second of acceleration, v= 0.5 × 3×108 m/sec (the speed of light) and v=at; plug in numbers... t= 1.5×107 seconds= 4167 hours = 173.7 days = 24.8 weeks of acceleration, or less than half a year. A second half a year of acceleration will be required to slow the ship down when it finally reaches its destination, so the interstellar power plant must have enough fuel to last at least 1 full year. While substantial, this is still an imaginable undertaking that ‘only’ requires a reactionless drive system. Getting to nearly the speed of light (minus losses due to relativity) would take a year speeding up and a year slowing down, but cut the time spent coasting nearly in half.
The Botany Bay, a sub-light Sleeper Ship
My personal favorite sleeper vessel is the Botany Bay from the original Star Trek franchise (“Space Seed”) which held a crew of genetically enhanced humans cryogenically suspended in low berths for 200 years. Traveller is a very flexible, adaptive system; this is my adaptation of a sleeper ship using Cepheus Engine rules. I am going to make a couple of changes to the standard rules to cope with scientific limitations not really envisioned by the general rules. First, sub-light engines cannot approach the speed of light; I am setting an arbitrary maximum at 50% of light speed. Secondly, when a ship is coasting between star systems it uses only 20% of the normally required power. I incorporate this idea using a secondary power plant sufficient for a ship ¹⁄₅ the size of the Botany Bay which will substantially decrease the fuel needed for a longer voyage.
As discussed previously, it takes about 24.8 weeks for a 1g gravitic engine to accelerate up to 50% of light speed. Since it also has to slow down, roughly 1 year of fuel is an absolute minimum a sleeper ship must have just to arrive at a safe velocity. A hydrogen-powered fusion reactor is barely possible for a one-year journey, but fortunately a more primitive powerplant with better characteristics for this particular use is already included in the standard rules (at least with my preferred Cepheus Engine ruleset). Fission power plants are twice as large, twice as expensive and require expensive radioactives as fuel, but they last much longer. Given the tonnage of hydrogen which will power a fusion reactor for one week, a fission reactor will use the same tonnage of radioactives over 26 weeks (per Cepheus Engine System Reference Document, p133).
Now that acceleration and deceleration are covered, the ship will spend most of its time coasting (at half the speed of light!) for years. Because one of the most energy-guzzling components will be shut down along with many of the other ship systems, a ship can get by with much lower power available (my arbitrary designation is 20%; your mileage may vary). For a 2000 ton vessel, 20% of that value gives a 400 ton effective size and thus requiring a Type B powerplant at 14 tons and 32 MCr that consumes 4 tons of radioactives per year. In order for the ship to have a 10 light year range (roughly a jump-3 starship), 20 years worth of radioactives (80 tons) will be needed to power the ship during its decades of coasting. It may take the Botany Bay a long time to get where it’s going and the ship may not have the fuel to return, but one-way interstellar travel using standard gravitic engines can be played.
A skeleton crew must stay awake during coasting to deal with general repairs and maintenance. For a colonial crew of 400, a one year of service maximum per appropriate sleeper seems a reasonable expectation for a 20 year journey. Twenty people may not be needed on the Botany Bay at one time, but accidents do happen and having extra capacity during emergencies and while in orbit is likely a good idea. Assuming nearly perfect recycling of water, preserved food is actually relatively space efficient, with 1 ton of food adequate for approximately 500 person-days of normal consumption (i.e., 2 kg/day) based on NASA astronaut consumption. Unfortunately, 20 years means 7300 days (not including leap years), and thus each active crewmember would need 14.6 tons of cargo space just for food (followed by waste storage). Agricultural space on board the Botany Bay that can recycle human wastes in a (mostly) sustainable fashion will be critical. Hydroponic growth chambers and space efficient vertical farming are available even today, but plants can’t shrink and algae can only grow so dense before it blocks the light. Even assuming significant efficiencies, it could easily take 30-35 dtons of volume to grow enough food for one person for one day on a continual basis. 350 tons of agricultural space should provide sufficient plant/algae volume to grow enough food (assuming efficient waste/water recycling) to cover the daily needs of a regular skeleton crew of 10. The greenhouse space will also provide seedlings and growth chambers useful for starting populations of Terran crops on an alien world. I have priced the greenhouse space at 0.1 MCr/ton as a ‘luxury’. I just hope those colonial mechanics like to garden as well!
The main crew will be suspended in low berths for almost all of the trip. The required crew size estimates for an interstellar settlement have been calculated by several scientists, but the assumptions made and the likelihood of survival for the colony give answers ranging from 98 individuals (JBIS 70(2), 2018 arXiv:1806.03856) to 14,000 (Acta Astronautica 97:16-29, 2014). The Botany Bay will struggle to carry enough supplies and initial food as it is, so I am choosing 400 crew (200 tons of low berths) and hope the colonists don’t run into any major issues along the way. I am also adding another 200 low berths (100 tons) for animals that the colonists can breed on their new world. Animals are an essential part of any sustainable ecosystem, and expecting a compatible biology on an alien planet is unreasonable.
In most other ways, the ship is unremarkable. Cargo and hangar space are large, but the colonists need to carry civilization with them so the space is still probably inadequate. All essential modular bays (fuel skimming/processing, ATV, mining, etc) must be redundant as failures will critically endanger the survival of the colony. Workshops aboard the colony ship will allow colonists to build or modify essentials to support the colony when the spare parts run out. I include each workshop as 4 tons and costing 0.3 MCr, but this is an arbitrary decision. Most of the other shipboard systems are the bare minimum required to make a functional spacecraft. It may not be luxurious, but ships like the Botany Bay and her siblings could allow a developing system the chance to access the stars before Jump technology revolutionizes interstellar travel and consigns sleeper ships to antique museums as historical anachronisms of a bygone era.
TL 8 Botany Bay Generation Ship
Using a 2000-ton hull (40 Hull, 40 Structure), the Botany Bay is designed for a pre-jump planet to colonize nearby systems. It mounts maneuver drive K, and power plant K, giving a performance of 1g acceleration and a type-D powerplant for minimal power coasting. 30 tons of radioactive fuel for 18 months of acceleration and 80 tons of radioactives for 20 years of coasting are available for the two fission power plants. Adjacent to the bridge is a computer Model 0. The ship is equipped with standard sensors (-4 DM). There are 10 staterooms for a skeleton crew and 600 low berths for 400 humans and 200 animal equivalents. The ship has 0 hardpoints and 0 tons allocated for fire control. Cargo capacity is 480 tons along with 350 tons of agricultural greenhouse space and 5 workshops. The hull is standard, and is not armored. The ship requires a skeleton crew of 8: 3 engineers, 2 pilots, 1 navigator, 1 sensors/comms, 1 medic and up to 12 additional temporary crew for various shipboard tasks. The ship carries 400 low passengers and 100 tons worth of cryogenically suspended animals. The ship costs MCr 705.7 (MCr 635.14 including discounts and fees) and takes 188 weeks to build.
| Botany Bay Generation Ship (TL 8) | ||
|---|---|---|
| tons | price | |
| hull, 2000 tons (40 Hull, 40 Structure) | 200,000,000 | |
| Type K fission P-Plant | 62 | 160,000,000 |
| atomic fuel 18 months for type K | 30 | 30,000,000 |
| Type D fission P-Plant | 14 | 32,000,000 |
| atomic fuel 20 years for type D | 80 | 80,000,000 |
| Type K M-Drive (thrust 1) | 19 | 40,000,000 |
| Bridge | 40 | 10,000,000 |
| Computer (Model 1, rating 5) Software (included) Maneuver 0 Library 0 |
30,000 | |
| Standard Sensors -4 DM (included in hull price) | ||
| 10 staterooms for active crewmembers | 40 | 5,000,000 |
| 5 workshops | 20 | 1,500,000 |
| 600 low berths (400 human, 200 animal) | 300 | 30,000,000 |
| cutter docks 4×50 ton | 200 | |
| 5×50 ton modular cutters (in docks and hangars) | 121,525,000 | |
| hangar for small craft repair/module exchange | 65 | 26,000,000 |
| 15 modules for cutters (10×30 tons + 5 in cutters) (1 research, 2 fuel, 2 AFV, 2 cargo, 3 mixed, 3 mining, 1 passenger, 1 medical) | 300 | 46,650,000 |
| 480 Cargo | 480 | |
| 350 agricultural greenhouse | 350 | 35,000,000 |
| Monthly maintenance*** | ||
| Monthly life support*** | ||
| Totals | 2000 | 705,705,000 |
| *** The monthy maintenance cost is meaningless as the ship coasts through deep space. An estimate of 3 tons of spare parts per year of travel seems reasonable. Life support cost is questionable, as the agricultural space provides a significant proportion of food, water, and air recycling for the skeleton crew. | ||
Other Traveller versions also have nearly feasible generation ships similar to the Botany Bay. In Mongoose 2nd edition, maneuver drives require 10% of the power plant size of fuel per month for both fission and fusion plants. For a 1g ship, a maneuver drive requires power points equal to 10% of the ship’s tonnage. Generating 8 points of power per ton, the fission plant would take up 1.25% of the ship and use 10% of that, or 0.125% of the ship’s mass, every month for the maneuver drive alone, along with power for the rest of the ship’s systems. 12 months of acceleration/deceleration would only use 1.5% of the ship’s mass for fuel, allowing all other fuel to power the rest of the ship’s systems. Those other systems use twice as much power as a 1g maneuver drive, so 3% of the ship’s mass for every year of the journey. (Note that this is very different from my assumptions of a reduced need for power during coasting.) A journey of 2 parsecs (~6.5 light years) would then require 13 years of coasting at 50% of the speed of light, with the extra time accelerating/decelerating and allowing for some maneuvers in the system. This requires 14×3 + 1.5 or 43.5% of the ship’s mass be used for fusion fuel. This is again possible, and does not require any changes to the engine rules as written to create a feasible generation ship. It does use a bit more than twice as much volume for engines/fuel than my modified Cepheus Engine rules would, so a larger ship may be needed to carry 400 colonists and their supplies to their new home. In Mongoose 2nd edition, however, 1g maneuver drives and jump-1 drives both appear at TL9 making generation ships unnecessary. Changing the TL of the maneuver drive slightly would be needed to make generation ships reasonable.
Getting Around—Slowly
Sub-light engines are necessary for nearly every ship in Traveller (with the possible exception of some X-boat designs). For games where players move from one main world to another, maneuver drives are just how one gets to the highport or away from a gravity well. Other games, however, may involve a lot more emphasis on reaching the distant bases and unexplored corners of planetary systems. These travels can be simplified using some assumptions based on geometry while still providing the sense that more remote worlds actually take some real time to reach. Whether the remote world is circling the same star or a nearby one, sub-light travel can get sophonts pretty much wherever they wish to go. It just may take a while.
 Freelance
Traveller
Freelance
Traveller