In-System Navigation
This article originally appeared in the July/August 2020 issue.
As discussed in previous articles, in-system travel is required a lot more than books seem to indicate. Travel to a world’s 100D will not provide a viable jump solution in many cases. Longer travel times are going to be normal, and we need to be able to somewhat accurately determine how long this takes.
Piracy is also a long-time staple of Traveller. Ships not near patrolled planets run the risk of pirates trying to get some free income. As described, the accuracy of a jump is poor at best; pirates cannot be waiting at a “jump point” for incoming traffic, and outgoing starships also have a fair amount of leeway to determine where they will jump. We need to know if and how fast a pirate can intercept a ship.
When a ship comes out of jump space it will have some velocity computed based on the relative motions of the stars and the velocity of the ship in relation to the source star (independent of standing or running jumps). Besides having that velocity there are no other effects from the jump. That is, the jump doesn’t magically affect the ship’s velocity vector – jumping within a system just changes the ship’s location, not its speed or direction of travel.
In our world with no constant-acceleration drives, travel from one planet to another is usually done via Hohmann transfer; a very low energy course that can only be attempted when planets are aligned properly, e.g., in an Earth-Mars Hohmann transfer, Mars needs to be 45░ in front of Earth. The ship leaves on a 4 AU curved course that eventually intersects Mars’ orbit 8.5 months later requiring only about a 3km/s velocity delta or 5 minutes of thrust from a Manoeuver-1 ship. Other transfers can be made with slingshot effects around planets gaining (or losing) velocity. (The energy comes from the planet’s energy at a proportional rate; the effect on any planet is unmeasurable). These allow for quite a variety of operations, albeit over a long time. The Messenger probe made 6 gravity assists over a 7 year period to arrive at Mercury.
Traveller, of course, has long-term constant acceleration ships. No Traveller starship is going to be spending 250 days doing nothing waiting to rendezvous with a different planet. With the same configuration between Earth and Mars (45░), the straight-line course is about 1AU. A ship can point itself about 6,000,000 km in front of where Mars is at that moment and accelerate for about 34.3 hours and decelerate just a bit longer time. As they need to slow down from Earth's orbital velocity of 30 km/s to Mars’ 24 km/s an extra 10 minutes of thrust is required. In that 68.7 hours Mars will have moved about 5,938,000km and the ship can then plot an orbital insertion vector.
Somewhat counter-intuitively travelling at twice the acceleration (M-2 ship) will not arrive in 1/2 the time. The same Earth-Mars trip would take about 48.6 hours (70% of the time) at 2G. At 6G the trip would take 28hours (40% of the time). The higher G ships would also need to aim closer to the planet as the trip is shorter.
Similarly slingshot and atmosphere braking manoeuvres are primarily for ships with no real drives, though a slingshot can change a high-speed ship’s vector that might take many hours of 1G thrust. In the above Earth-Mars manoeuvre the ship may be going at the required 24 km/s but it is at a significant angle to Mars’ orbit. A slingshot (Gravity assist) can correct the course to be along the orbital line.
Most Traveller systems show travel times using equation [7] (see box below) – accelerate for half the distance and then turn-over so the ship is pointing the other direction and decelerate the remaining half. Using the constant acceleration formula (equation [8]) accelerating all the way to the destination results in a shorter time, but at the end of the journey one doesn’t want to be travelling at 1200 km/s and unable to interact with the destination (unless firing a few missiles is your goal).
In-system travel is slow, despite being much faster than real-world travel. Micro-jumps (jumping in-system) can be much faster. A jump takes 168 hours (7 days) ▒10%. At 1G a 168-hour trip (with turnover) will cover 900 million km, or about 6 AU and easily get a ship to Jupiter, but if you needed to travel from Earth to Saturn (8 to 11 AU, depending on where in their orbits the two planets are), jumping would be faster (albeit taking more fuel).
Gas Giant refueling is seen as a cheap way for ships to get fuel, rather than paying local star ports or star bases for refined fuel. The captain needs to consider just how far away that Gas Giant is. For Sol, Earth (and the Sun’s 100D limit) are both near 1AU, while Jupiter is 5-5.5 AU from the sun. Depending on planetary alignment, that means that the straight-line distance between Earth and Jupiter can be 4 to 6.5AU. Likely better to pay for the fuel than take the extra 6 days. Similarly, getting ice from the asteroids will still add 3.5 days in the Sol system. Of course, some planets like Regina in the Spinward Marches actually orbit a gas giant.
As long as all the units of all the values agree the equations will work; you do not need to use any particular system of units (like SI). Constants, such as G force, also must be expressed in units that agree with the other values. As most calculations use kilometers (km) (instead of meters, m) we would want to use 0.0098 km/s2 as our 1G value, and while travel times in hours are more applicable, we can use 127137.6 km/h2. Mixed units (e.g., 1G = 35.304 kilometers per hour per second (one second of acceleration gives a 35 km/h speed change)) can be used carefully; they are more likely to cause problems than make the solution easier.
Piracy
In order for piracy to be effective the pirates need to be able to intercept a starship before it gets to a point where it can get assistance from the local government. Some planets are low-tech and/or don’t have ships outside of orbit (e.g., for customs inspections); in these cases a pirate could lurk out at about 10 planetary diameters (Geosynchronous orbit for Earth is about 3 planetary diameters) and intercept their targets easily.
In order for pirates to make good on their attack, they need to be able to board the target spacecraft; this can be after a successful attack, or as part of it. A ship at the half-way point (or just entering the system – using a running jump) will be at its maximum velocity; disabling a ship’s engines when it is travelling at 150km/s would require 4.25 hours at 1G acceleration to match course and it will have travelled 2,300,000 km towards the planet (180 Earth planetary diameters). As long as the pirates have significantly higher manoeuvre drives and are closer to the planet they should have no issue intercepting.
While there is no “optimum” jump point that starships use to enter/leave jumpspace (and as mentioned earlier they will be at maximum velocity at this point), there is an optimum region, a general direction (cone-shaped) from which the jump manoeuvre is optimized. This location is not fixed, but changes based on where the source and destination planets are in their orbits, and of course is different for each star system and will be millions of kilometers across.
Also as mentioned in a previous article, most jumps (~89% of trips to worlds in the habitable zone) will be to the star’s 100D limit. This increased travel time makes the pirates’ job much easier, as they can hang out ż of the way from the star’s 100D limit to the planet and have a good chance of intercepting a ship, assuming of course that the pirate’s maneuver drive is better. System patrols can also match this location, but they need to be in every location; that is if there are 3 nearby star systems and 2 points of interest in a system, patrols need to be in at least 6 places.
The target ship will be on a high-velocity vector towards the planet, ideally slowing down all the way to near the planet. Turning is very much out of the question, but accelerating instead could make interception difficult for the pirates. The pirates can almost certainly plot a course to intercept if they can detect the ship, but matching velocities so that they have more than one or two shots and are able to board will be more difficult and depend on the actions of the ship’s captain.
General Rules
Rules for this are very difficult to abstract, because a number of very important values are situationally dependent. The relative velocities of the two stars and both planets, as well as the distance to the jump point, will determine the initial velocity which could make interception easy or difficult. Inaccuracies in navigation should also add some additional uncertainty to the initial situation.
Assuming that the data for the stellar and planetary locations and vectors are known, there is further complication as these examples only use straight line, single-dimension equations (which is acceptable if at least one of the source or destination planets has large choice of their vector, e.g., there is no masking). The ship can plot a course that can be quite linear. Otherwise the vector will need to be split out into 3 components: radial and orbital on the ecliptic and a stellar polar component. The latter is the easiest to minimize and solving the problem in 2 dimensions would likely give acceptable results, however no one is likely to do the math required to be totally accurate.
There is one simple approximation that can be applied. We previously discussed how a running jump can reduce travel time by 30%; we can actually look at the entire travel through both systems and a jump as one. Let’s assume one is going from Regina (10.3 million km to the jump point) to a planet masked by its star and a 5 million km trip. Standard Traveller would calculate 2 standing trips for 18 hrs (Regina to jump entry), and 12 hrs (jump exit to destination) = 30hrs. Two running trips would be outbound-accelerating for 12.7 hrs and inbound-decelerating for 8.9 hrs = 21.6 hrs, and is what we suggested last time; however, due to the difference in times accelerating and decelerating the net speed change is significant, possibly offset by stellar/planetary motion, but could be off by 100s of km/s and result in a flyby of the target world. A more general solution is to calculate one trip of 15.3 million km which gives 21.9 hrs – accelerate for 11 hours, turn around and decelerate for 1.7 hours more then jump and continue decelerating to the target.
In summary, we can estimate a trip using a running jump by taking the total distance in both systems and use the normal Traveller travel time (eq. [7]), instead calculating the time on each side of the jump. Piracy is quite possible as long as the pirate has a significantly higher manoeuvre drive and the ship does not use the planet’s 100D limit for approach. Gas giant refueling is likely too long of a detour to make it worthwhile.
The Math
The formulas used are in the box below. Let’s look at a real-world example. Epsilon Eridani (ε Eri, Shulimik in Traveller) is about 3.2pc from Sol (4 hexes in Traveller), chosen as it is close to the ecliptic and thus the jump route will be masked by Sol’s 100D limit about 40% of the time. It has a relative motion from sol of 962 mas/yr or 460.5 million km/yr = 14.6km/s plus 15.5km/s radial velocity. Using Pythagoras gives it 21.3km/s (away at an angle). As its (real world) planets are more than 3AU from the star, the jump will be from the planet’s 100D limit. We are also assuming no origin stellar masking which is a really insignificant possibility at 3AU. Assuming the main planet ε Eri II is a LGG the travel distance to 100D (planetary) would be about 8.5 million km. Using eq. [8] and 1G acceleration that gives a time of 41700s and a running jump velocity of 409 km/s. Furthermore the ship can jump from any direction as it is only a planetary 100D limit. Planets near or inside the stellar 100D limit will have little effective choice on direction.
| Equations Referenced | ||
| Description | Formula | |
| Equations of motion in a straight line;D=distance, t=time, V=velocity a = acceleration;a 0 subscript (e.g., V0) is initial; a 1 subscript (e.g., V1) is final. | [1] | V1 = V0 + at |
| Solve for t: | [2] | t = (V1-V0)/a |
| [3] | D1 = D0 + V0t + Żat2 | |
| [4] | D1 = D0+Ż(V0+V1)t | |
| [5] | D1 = D0 + V1t - Żat2 | |
| [6] | V1 = √(V02 + 2a(D1—D0)) | |
| Constant acceleration time with no net velocity change – standard Traveller formula | [7] | t = 2√(D/a); V1 = V0 = 0 |
| Constant acceleration – velocity change | [8] | t = √(2D/a); V1 = at, V0 = 0 |
| Simple interception: ap = pursuer acceleration; at = target acceleration | [9] | t = 2V0/(ap - at) |
| Interception at a distance and acceleration to optimize pursuer speed. | [10] | t = (V0▒√(2D0(at - ap) + V02))/(ap - at) |
| [11] | ap = at + V02/2D0 |
Running jumps help with the transit time by not “zeroing” the velocity relative to the original planet, but not all directions are equivalent. If the course is not masked by the star then any angle is permitted allowing for the greatest flexibility of vectors in the destination system. Consider Venus at 0.72AU; it is within the 100D limit of the Sun (0.93AU, or if you use the revised values from the first article in the series 0.96AU). Travelling to the point closest on the 100D limit is about 36 million km (24 hrs) and only allow jumping with a narrow range of vectors. Any significant change in vector will require travelling millions of additional km and will not save that much time on the other end, to the extreme of selecting the opposite vector requiring a 251 million km trip (63 hrs).
If the earth is on the near-side of the sun with respect to ε Eri and not masked then the best solution would be to jump to the 100D limit of Earth and have a 1.2 million km trip to the planet – in which case the running jump is far too fast. At 4pc distance this level of accuracy is frankly impossible – unequal heating of the ship’s surface would give more than a 2.5 million km error, besides as previously mentioned the vast majority of trips wouldn’t even have this as an option. To further drive this point home (as it has quite an impact in Traveller), a 300m bulk carrier on the ocean needs to adjust its course from Boston to NY when leaving Europe, which it can do any point in the trip, (1 degree). This means the rear of the ship need to move about 2.5 m to correct the course. A 300m Traveller ship needing to change course from just missing to intersecting a 100D planetary at 4pc (1 mas) would need to move its rear by 2 microns – ╝ of a red blood cell.
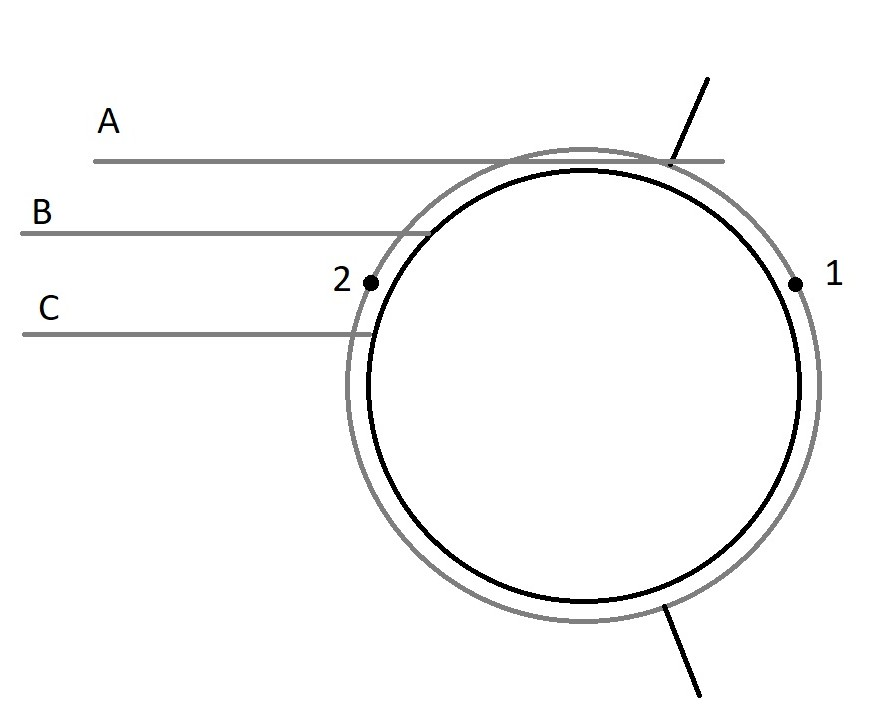 In this diagram ε Eri is to the left. (Author’s note: this is
schematic, not to scale.) There are two positions for the planet (1)
masked by the inner circle representing the 100D limit of Sol, and (2)
not masked. Three vectors in from ε Eri (A) which just skirts the 100D
limit and ends somewhere in front of position (1) just outside of the
orbital path with a timed exit from jumpspace. (B) which impacts the
100D limit just behind position (2) and (C) which impacts just ahead of
position (2). The lines are shown parallel as the other star is so far
away, but actually would have an angle of about 125 mas (0.00003
degrees) with respect to one another. This further illustrates how small
angular perturbations can cause large differences several parsecs away.
This is in 3D of course so one could plot other courses (not shown)
above/below the planet. Which would in effect be a circle projected onto
the 100D sphere of the star.
In this diagram ε Eri is to the left. (Author’s note: this is
schematic, not to scale.) There are two positions for the planet (1)
masked by the inner circle representing the 100D limit of Sol, and (2)
not masked. Three vectors in from ε Eri (A) which just skirts the 100D
limit and ends somewhere in front of position (1) just outside of the
orbital path with a timed exit from jumpspace. (B) which impacts the
100D limit just behind position (2) and (C) which impacts just ahead of
position (2). The lines are shown parallel as the other star is so far
away, but actually would have an angle of about 125 mas (0.00003
degrees) with respect to one another. This further illustrates how small
angular perturbations can cause large differences several parsecs away.
This is in 3D of course so one could plot other courses (not shown)
above/below the planet. Which would in effect be a circle projected onto
the 100D sphere of the star.
Earth has an orbital speed of 30 km/s so in order to enter orbit a ship needs to be at that speed along the vector that Earth is currently using. In general, approaching from in front of the planet is slightly quicker despite having to slow down to 0 and reverse back up to 30km/s rather than just slow down to 30 initially, but this is where a slingshot to change direction is useful and results in a better overall speed.
The first step is determining the parameters of the running jump. Leaving a size 2 planet outside of the star’s 100D limit will have an open vector direction but a sub-100 km/s (plus stellar motion) velocity. A gas giant will also typically be open to any course and a 250-500 km/s potential velocity. A masked planet, say Venus in Sol or Earth in configuration (1) in the diagram will have a very limited vector, but speeds up to the 750-1500 km/s range.
We then compare this to the destination planet parameters, which may limit the maximum entry speed as there is less time to decelerate to the planet. In our example the travel time from Sol’s 100D limit to Earth is 6 million km or a bit more depending on how close the course is. This limits the max speed as entering not too much faster than 343 km/s, where our maximum exit speed was 409 km/s. These speeds are determined by equation [8].
To calculate the exact time, we would now need to do a lot of math that no-one who was not in a space ship would do. Besides splitting into 3 components, these values are all highly dependent on the exact geometry of the two systems (unknown) and where the jump came out (semi-random) and as the planet is not travelling in a straight line (the time scales are long enough that making the approximation of an orbit as a line will give poor results), translating everything to polar coordinates would likely be advised.
Course (B) and (C) in the diagram are close to the planet, and 343 vs 409 km/s are close enough that we can just assume that the integrated travel time calculation is good enough.
Course (A) is much longer about 110 million km, and could still use the integrated travel time, but with any constraints on leaving there would be an additional estimate of the speed lost due to course correction. A 30░ course difference from a straight line would likely have a sin(30░) = 0.5 or 50% correction to the 409 km/s vector. Using [eq 2] (409*50%)/a = 5.8 hour more time.
Let’s look at pirates in the case of course A. The reasonable area where the ship could appear is likely in a 40 million km polar arc near the 100D limit of Sol and likely up to 40 million km wide as well – any of these positions would provide reasonably similar solutions to approach Earth at most adding a few hours to the trip. Potential pirates have a large area in which to hide. Assuming that there is no patrols nearby and the pirates in a manoeuvre-2 detect a ship inbound it will take them 5.75 hours to reach the 408 km/s entry speed from a relative standstill, however by that time the target ship has not only covered more distance, but is now travelling at 612 km/s as it is still accelerating. We could iteratively figure out where the pirates would intercept the ship, but we can use [eq 3] for each ship expressing the distance from the jump entrance: The pirates are D1 = D0 + 0t + Żapt, while the target is D1 = 0+408t+ Żatt. The pirate will intercept when D1 is the same for both thus we have D0 + Żapt = V0t + Żatt this gives us [eq 9 and 10]. We assume that D0 is 0 for the pirate though it may be millions of km away at the jump point, the intercept course will be plotted to intersect the path of the target, and will be effectively the same length. Using [eq 9] gives us a solution of 23 hours.
The target captain has options available to him, while it is difficult and ineffective to change the course, they can choose to continue accelerating/decelerating or not. In the previous example the ship is past the turn-over point and is decelerating to Earth – so in fact we would need to adjust the time downwards. They can stay their course, or they can accelerate. In this particular example at the intercept point the pirates have a speed of 1622 km/s and the target 1219 km/s likely only enough time for a few shots, and if the target is armed staying the course could be best. On the other hand switching over to acceleration as soon as the pirates are detected will mess up their speed at the planet, but will draw out the intercept to much closer to the planet where presumably help is available.
Should the pirates be closer to the planet they can actually get better results. [eq 10] has two solutions (the +/- in the formula). Let’s say the pirates are 8 million km closer (D is positive) we solve to get 8.77 or 14.3 hrs. The first number is where the ship overtakes the pirates (remember the course is 2D so they don’t really “pass” the pirate ship), the second is when the pirates intercept. If we increase D0 to 12 million km, the radical is the root of a negative number, which is impossible – this means that the pirate ship due to its superior acceleration pulls away from the target before they ever cross paths. Of course the acceleration doesn’t need to be at max. Using [eq 11] we can calculate that the optimum acceleration for the pirate is in fact ap = 1.71 G. Re-working the intercept formula and we get 16.4 hours. Not only that the speeds are much closer together limiting the options for the target.
For a final example lets look at an interplanetary pirate interception. The target leaves Earth for Jupiter and there is a pirate in the asteroid belt. Jupiter is 5 AU from earth’s orbit on average. The asteroid belt is about 2.3 AU from Jupiter. The target has passed the turn-over point and is decelerating towards Jupiter. Their speed at the turn-over 2.5 AU (374 million km) from Jupiter is 2707 km/s after some 76.7 hours. Putting the values in and remembering that at is negative we get 2 numbers: 3.3 hrs (when the target passes the asteroid belt) and 47.86 hours. The speeds at this point are 3377 km/s for the pirate and 1018 km/s for the target – a very short encounter time. So the pirate wants to accelerate at max for some time, then accelerate slower to encounter at a later point with less difference in velocity. There are no simple formulae for this; it is better for the referee to plot courses and determine position and speeds iteratively using the provided formula.
Piracy in Traveller is quite possible, particularly as ships don’t usually travel in from a planet’s 100d limit. Computing anything accurately requires a lot of math, but we can approximate to within a half-hour quite easily with the provided equations.
 Freelance
Traveller
Freelance
Traveller